Denominamos discriminante o radical b2 - 4ac que é representado pela letra grega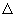 
(delta).
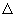(delta). |
Podemos agora escrever deste modo a fórmula de Bhaskara:
 |
De acordo com o discriminante, temos três casos a considerar:
1º Caso: O discriminante é positivo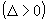 
.
.
O valor de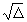 
é real e a equação tem duas raízes reais diferentes, assim representadas:
é real e a equação tem duas raízes reais diferentes, assim representadas: |  |
Exemplo:
- Para quais valores de k a equação x² - 2x + k- 2 = 0 admite raízes reais e desiguais?
SoluçãoPara que a equação admita raízes reais e desiguais, devemos ter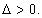
Logo, os valores de k devem ser menores que 3.
2º Caso: O discriminante é nulo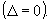 
O valor de 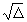é nulo e a equação tem duas raízes reais e iguais, assim representadas:
é nulo e a equação tem duas raízes reais e iguais, assim representadas:
Exemplo:
- Determine o valor de p, para que a equação x² - (p - 1) x + p-2 = 0 possua raízes iguais.
.
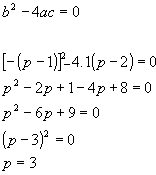
Logo, o valor de p é 3.
3º Caso: O discriminante é negativo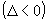 
.
.
O valor de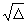 
não existe em IR, não existindo, portanto, raízes reais. As raízes da equação sãonúmero complexos.
não existe em IR, não existindo, portanto, raízes reais. As raízes da equação sãonúmero complexos.
Exemplo:
- Para quais valores de m a equação 3x² + 6x +m = 0 não admite nenhuma raiz real?
Para que a equação não tenha raiz real devemos ter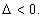 
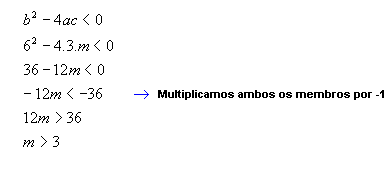
Logo, os valores de m devem ser maiores que 3.
Resumindo
Dada a equação ax² + bx + c = 0, temos:
Para
 , a equação tem duas raízes reais diferentes.Para  , a equação tem duas raízes reais iguais.Para  , a equação não tem raízes reais. |
0 comentários:
Postar um comentário