Considere a equação ax2 + bx + c = 0, com a 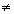 0 e sejam x'e x'' as raízes reais dessa equação.
0 e sejam x'e x'' as raízes reais dessa equação.
Logo: 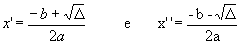
Observe as seguintes relações:
- Soma das raízes (S)
- Produto das raízes (P)
Como 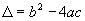 ,temos:
,temos:
Denominamos essas relações de relações de Girard. Verifique alguns exemplos de aplicação dessas relações.
- Determine a soma e o produto das raízes da equação 10x2 + x - 2 = 0.
Solução
Nesta equação, temos: a=10, b=1 e c=-2.
A soma das raízes é igual a 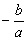 . O produto das raízes é igual a
. O produto das raízes é igual a 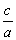
Assim: 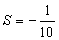 Assim:
Assim: 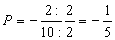
- Determine o valor de k na equação x2 + ( 2k - 3)x + 2 = 0, de modo que a soma de suas raízes seja igual a 7.
Solução
Nesta equação, temos: a=1, b=2k e c=2.
S= x1 + x2 = 7
Logo, o valor de k é -2.
- Determine o valor de m na equação 4x2 - 7x + 3m = 0, para que o produto das raízes seja igual a -2.
Solução
Nesta equação, temos: a=4, b=-7 e c=3m.
P= x1. x2= -2
Logo, o valor de m é 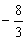 .
.
- Determine o valor de k na equação 15x2 + kx + 1 = 0, para que a soma dos inversos de suas raízes seja igual a 8.
Solução
Considere x1 e x2 as raízes da equação.
A soma dos inversos das raízes corresponde a 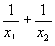 .
.
Assim:
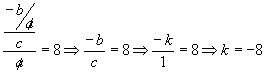
Logo, o valor de k é -8.
- Determine os valores de m para os quais a equação ( 2m - 1) x2 + ( 3m - 2) x + m + 2 = 0 admita:
a) raízes simétricas;
b) raízes inversas.
Solução
Se as raízes são simétricas, então S=0.
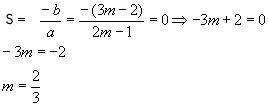
Se as raízes são inversas, então P=1.
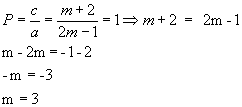






1 comentários:
Muito boa a explicação. Achei falta de exercícios.
Postar um comentário