Semelhança de Polígonos
Introdução
Observe as figuras:
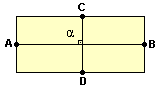
Figura A
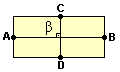
Figura B
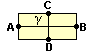
Figura C
Elas representam retângulos com escalas diferentes. Observe que os três retângulos tem a mesma forma, mas de tamanhos diferentes.
Dizemos que esse mapas são figuras semelhantes.
Nessas figuras podemos identificar:
AB - distância entre A e B (comprimento do retângulo)
CD - distância entre C e D (largura do retângulo)
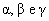- ângulos agudos formados pelos segmentos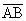 
CD - distância entre C e D (largura do retângulo)
- ângulos agudos formados pelos segmentos
Medindo os segmentos de reta 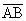e 
e os ângulos () das figuras, podemos organizar a seguinte tabela:
e e os ângulos (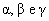) das figuras, podemos organizar a seguinte tabela:m ( ) | m ( ) | ângulo | |
| Fig. C | 3,9 cm | 1,3 cm |  = 90º |
| Fig. B | 4,5 cm | 1,5 cm |  = 90º |
| Fig. A | 6,0 cm | 2,0 cm |  = 90º |
Observe que:
- Os ângulos correspondente nas três figuras têm medidas iguais;
- As medidas dos segmentos correspondentes são proporcionais;
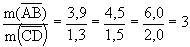
Desse exemplo, podemos concluir que duas ou mais figuras são semelhantes em geometria quando:
- os ângulos correspondentes têm medidas iguais ;
- as medidas dos segmentos correspondentes são proporcionais;
- os elementos das figuras são comuns.
Outro exemplos de figuras semelhantes:
têm formas iguais e tamanhos diferentes.
0 comentários:
Postar um comentário