As equações do 2º grau na variável x que possuem alguns coeficientes ou alguns termos independentes indicados por outras letras são denominadas equações literais.
As letras que aparecem numa equação literal, excluindo a incógnita, são denominadas parâmetros.
Exemplos:
ax2+ bx + c = 0 incógnita: x
parâmetro: a, b, c
ax2 - (2a + 1) x + 5 = 0 incógnita: x
parâmetro: a
Equações literais incompletas
A resolução de equações literais incompletas segue o mesmo processo das equações numéricas.
Observe os exemplos:
- Resolva a equação literal incompleta 3x2 - 12m2=0, sendo x a variável.
Solução
3x2 - 12m2 = 0
3x2 = 12m2
x2 = 4m2
x=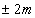
Logo, temos: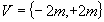 
- Resolva a equação literal incompleta my2- 2aby=0,com m
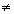0, sendo y a variável.
Solução
my2 - 2aby = 0
y(my - 2ab)=0
Temos, portanto, duas soluções:
y=0
ou
my - 2ab = 0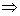 
my = 2ab 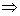y= 
my = 2ab y=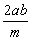
Assim:
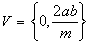
Na solução do último exemplo, teríamos cometido um erro grave se tivéssemos assim resolvido:
my2 - 2aby= 0
my2 = 2aby
my = 2ab
Desta maneira, obteríamos apenas a solução .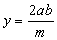
.
O zero da outra solução foi "perdido" quando dividimos ambos os termos por y.
Esta é uma boa razão para termos muito cuidado com os cancelamentos, evitando desta maneira a divisão por zero, que é um absurdo.
As equações literais completas podem ser também resolvidas pela fórmula de Bhaskara:
Exemplo:
Resolva a equação: x2 - 2abx - 3a2b2, sendo x a variável.
Solução
Temos a=1, b = -2ab e c=-3a2b2
Portanto:
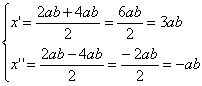
Assim, temos: V= { - ab, 3ab}.
0 comentários:
Postar um comentário