PROBLEMAS DO 2º GRAU

Postado por Ismael Alexandre | Marcadores: Equações de 2º grau

Para resolução de problemas do 2º grau, devemos seguir etapas:

Sequência prática

Estabeleça a equação ou sistema de equações que traduzem o problema para a linguagem matemática.
Resolva a equação ou o sistema de equações.
Interprete as raízes encontradas, verificando se são compatíveis com os dados do problema.

Observe agora, a resolução de alguns problemas do 2º grau:

Determine dois números inteiros consecutivos tais que a soma de seus inversos seja .

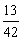Solução

Representamos um número por x, e por x + 1 o seu consecutivo. Os seus inversos serão

representados por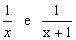

Temos estão a equação: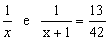

Resolvendo-a:

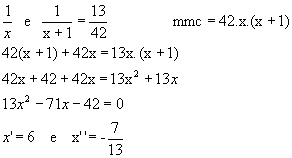
Observe que a raiz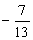

não é utilizada, pois não se trata de número inteiro.

Resposta: Os números pedidos são, portanto, 6 e o seu consecutivo 7.

Um número de dois algarismos é tal que, trocando-se a ordem dos seus algarismos, obtém-se um número que o excede de 27 unidades. Determine esse número, sabendo-se que o produto dos valores absolutos dos algarismos é 18.

Solução

Representamos um número por 10x + y, e o número com a ordem dos algarismos trocada por 10y + x.

Observe:

Número: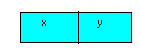

10x + y

Número com a ordem dos algarismos trocada: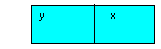

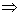10y + x.

Temos, então, o sistema de equações:

Resolvendo o sistema, temos:

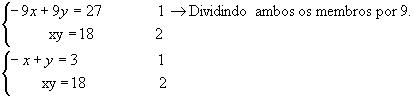
Isolando y em 1 :

-x + y = 3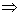

y= x + 3

Substituindo y em 2:

xy   = 18
x ( x + 3)      =   18
x² + 3x     =   18
x² + 3x - 18   =   0
x'= 3 e x''= -6

Determinando y para cada um dos valores de x, obtemos:

y'= 3 + 3 = 6

y''= -6 + 3 = -3

Logo, o conjunto verdade do sistema é dado por: V= { (3,6), ( -6, -3)}.

Desprezando o par ordenado de coordenadas negativas, temos para solução do problema o número

36 ( x=3 e y=6).

Resposta: O número procurado é 36.

Duas torneiras enchem um tanque em 6 horas. Sozinha, uma delas gasta 5 horas mais que a outra. Determine o tempo que uma delas leva para encher esse tanque isoladamente.

Solução

Consideremos x o tempo gasto para a 1ª torneira encher o tanque e x+5 o tempo gasto para a 2ª torneira encher o tanque.

Em uma hora, cada torneira enche a seguinte fração do tanque:

Em uma hora, as duas torneiras juntas encherão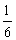

do tanque; observe a equação correspondente:

Resolvendo-a, temos:

6( x + 5 ) + 6x = x ( x + 5 )

6x + 30 + 6x = x²+ 5x

x² - 7x - 30 = 0

x'= - 3 e x''=10

Como a raiz negativa não é utilizada, teremos como solução x= 10.

Resposta: A 1ª torneira enche o tanque em 10 horas e a 2ª torneira, em 15 horas.

Num jantar de confraternização, seria distribuído, em partes iguais, um prêmio de R$ 24.000,00 entre os convidados. Como faltaram 5 pessoas, cada um dos presentes recebeu um acréscimo de R$ 400,00 no seu prêmio. Quantos pessoas estavam presentes nesse jantar?

Solução

Podemos representar por: